
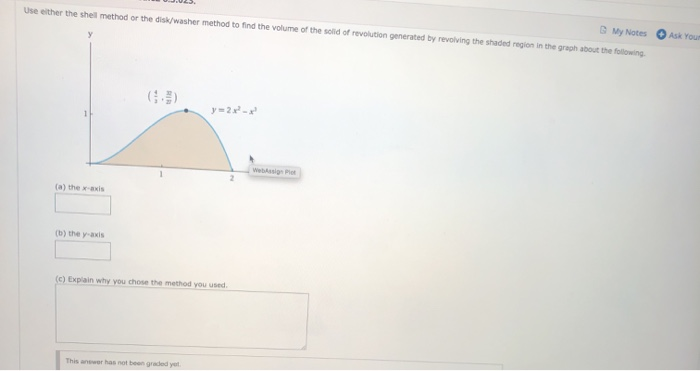

In certain examples the disk method doesn't work because there's a hole in the middle of the solid, but the outer and inner radii values of the washer slice are x-values in the domain of a single function. If the functions are given as y = f ( x ), we change them to x = f ( y). When we revolve about the y-axis, we integrate with respect to y. Note: In all cases so far, we revolved about the x-axis so we integrated with respect to x in all of them. Where f ( x ) is the outer or larger radius, g ( x) is the inner or smaller radius, and a, b are the x-values of the points of intersection for the curves. These two curves meet at (0, 0) and (1, 1) as shown, causing each slice to be a washer - a disk with a hole in the middle of it. Now let's consider a solid made by revolving the area between y = x² and y = x 1/ 2 about the x-axis. The previous case was simple since each disk was solid (no hole in the middle). We'll take the chunk of y = x ½ from x = 0 to x = 4 and we'll revolve it about the x-axis Let's do an example and then we'll discuss the approach. The volume of the solid is the sum of the volumes of all these cylinders, and, as usual in integral calculus, we limit the thickness of the slice to zero, then sum (or integrate) over the interval indicated. To find the volume of such a solid using the disk method, we use the fact that every cross sectional slice, cut perpendicular to the axis of revolution, is a cylinder.
A solid of revolution is the circular solid formed when an area of the plane is revolved around a given line of symmetry or axis.


 0 kommentar(er)
0 kommentar(er)
